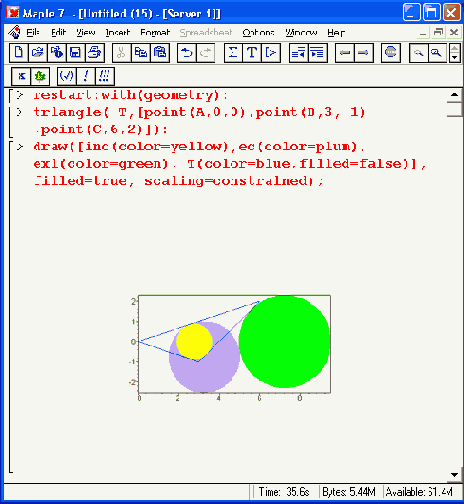
Примеры применения функции plot_real_curve
Шаг 2
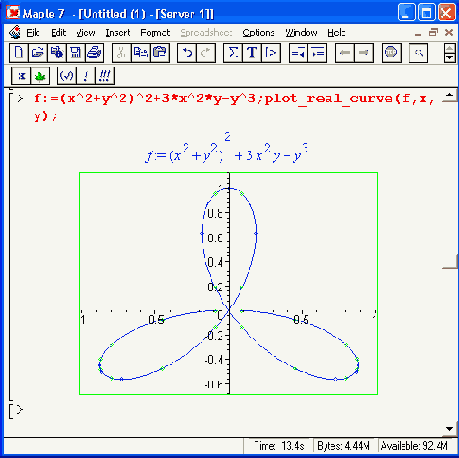
Рисунок 16.8. Примеры применения функции plot_real_curve
Шаг 2
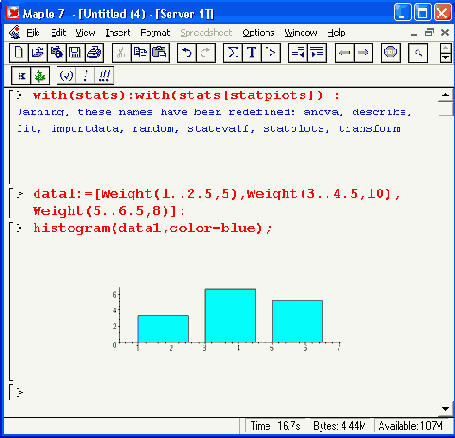
Обратите внимание на то, что для второго примера гистограмма будет несколько меняться от пуска к пуску, так как данные для ее построения генерируются случайным образом.
Шаг 2
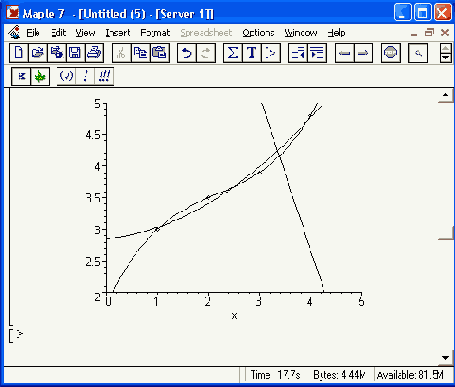
Рисунок 16.15. Примеры регрессии полиномом и первой, второй и третьей степени
В данном случае уравнение регрессии задано в виде z = a + bx + cy. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в не вычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у:
К сожалению, функция fit неприменима для нелинейной регресии. При попытке ее проведения возвращается структура процедуры, но не результат регресии — см. пример ниже:
Шаг 2
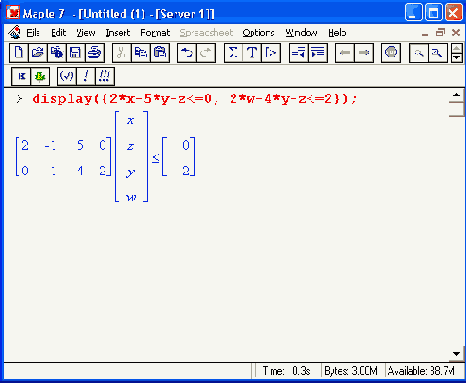
> dual( x-y,{2*x+3*y<=5.3*x+6*y<=15},z);
115zl +5z2, {1_<3z1+2z2,-l_<6z1+3z2}
Функция feasible может быть задана в трех формах:
feasible(C)
feasible(C,vartype)
feasible(C,vartype,'NewC','Transform')
Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:
> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);
true
> feasib1e({2*x+3*y<-5, 3*х+б*у<—15}, NONNEGATIVE);
false
Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:
Шаг 2
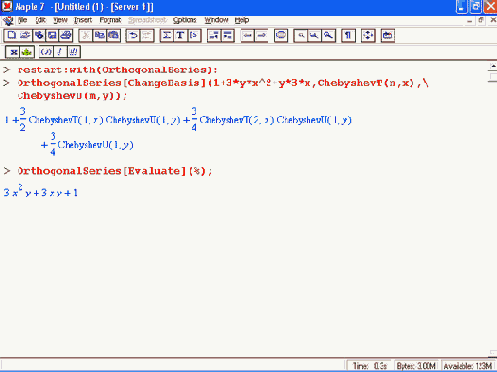
Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору:
> S:=Create((-irn/n!,ChebyshevT(n,x));
Шаг 2
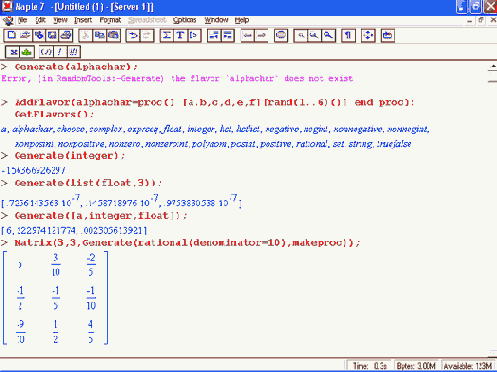
Функция GetFlavor(flvr) представляй случайный объект (или объекты) в форме процедуры:
> AddF1avor(a = rand(1..20)):
Generate(a):
15
> GetFlavor(a);
procO localt; global_seed;
_seed := irem(ax_seed,p);
t :=_seed;
toconcats do_seed:=irem(ax_seed,p);
t := sxt + _seed end do ;
irem(t, divisor) +offset endproc
> GetFlavor(integer);
module () localDefaults;
exportMain;
end module
Другая функция GetFlavors () возвращает все типы случайных объектов:
> GetFlavorsO;
a, alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Функция HasFlavor(flvr) служит для проверки наличия объекта данного типа в списке типов объектов, а функция RemoveFl avor(f1vr) — для удаления типа объекта. Следующие примеры иллюстрируют применение этих функций:
> HasFlavor(a):
true
> RemoveFlavor(a);
> HasFlavor(a):
false
> GetFlavors();
alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Обратите внимание на то, что после уничтожения объекта типа а он исчез из списка, выводимого функцией GetFlavors. Этот пакет, несмотря на довольно специфические возможности, наверняка будет полезен тем читателям, которые всерьез заняты реализацией «продвинутых» методов Монте-Карло, основанных на моделировании случайных объектов и ситуаций. Он служит серьезным дополнением к пакету статистических расчетов stats, описанному в этом уроке выше.
Шаг 2
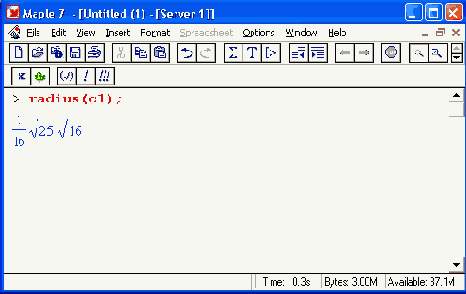
Шаг 2