с магнитным полем показывает, что

Шаг 3

Моделирование движения заряженной частицы в пространстве с магнитным полем показывает, что для принятых для моделирования параметров решаемой задачи, движение частицы происходит по спиралеобразной траектории. Получен как график траектории движения частицы, так и аналитические уравнения, описывающие это движение.



Шаг 3

Рисунок 17.17. АЧХ фильтра на операционной усилителе
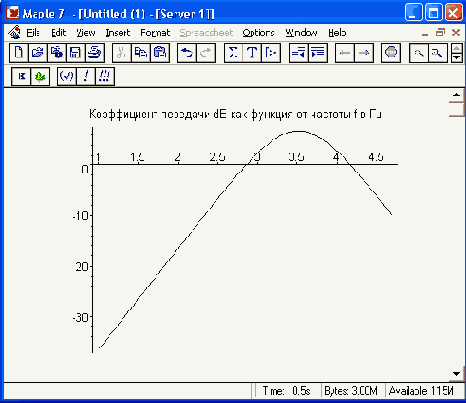
Далее построим фазо-частотную характеристику фильтра как зависимость фазы в радианах от частоты f в Гц:
> plot ([log10(f),phase, f=10..50000], color=black, title=*Фазо-частотная характеристика фильтра*);
Фазо-частотная характеристика (ФЧХ) фильтра показана на Рисунок 17.18
На ФЧХ фильтра можно заметить характерный разрыв, связанный с превышением фазовым углом граничного значения я. Такой способ представления фазового сдвига общепринят, поскольку его изменения стремятся вписать в диапазон от -я до п.



Шаг 3

Переменные напряжения на узлах схемы находятся из аналитического решения данной системы. При этом заблокируем вывод их аналитических значений, поскольку он очень громоздок. Тем не менее вы можете посмотреть на полученные формулы, поставив знак точки с запятой вместо знака двоеточия в приведенных ниже выражениях:
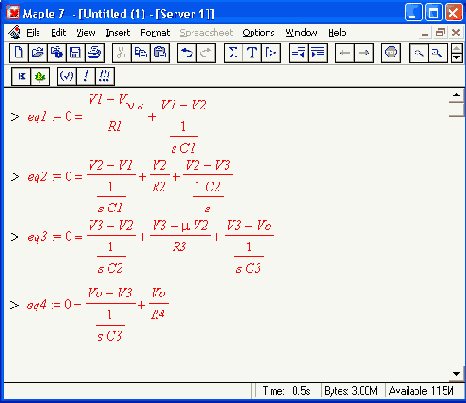
> solve({eql,eq2,eq3.eq4}б{Vl,V2.V3,Vo}):
Обеспечим присвоение переменным Vo, VI, V2 и V3 найденных из решения системы уравнений значений:
> assign(%):
Теперь найдем операторную передаточную функцию в аналитическом виде:



Шаг 3

Рисунок 17.19. Импульсная характеристика цифрового фильтра
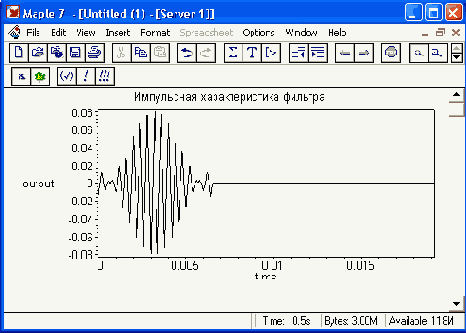
Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:
> rо := array (1..T+1): io := arrayd. .T+l):
> for n from 0 to Т do ro[n+l] :- y[n]; io[n+l] := 0; od:
> FFT(m,ro,io):
Построим график АЧХ фильтра:
> р :=[seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]:
> plot(p, frequency=0..fs/2, tabels=[frequency,gain], tit1e='AЧX фильтра',со1ог=black);
Он представлен на Рисунок 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).



Шаг 3

Рисунок 17.26. Временные зависимости напряжения на туннельном диоде и тока
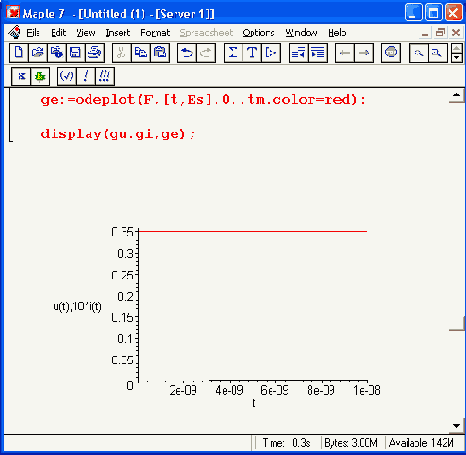
Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:
> gv:=plot({Id(Ud),(Es-Ud)/Rs},Ud=-.05..0.75,color=black,
labels=[Ud,Id]):
> gpp:=odeplot(F.[u(t),i(t)],0..tm,color=blue): 
> display(gv,gpp);
Фазовый портрет колебаний показан на Рисунок 17.27.



Шаг 3

Рисунок 17.2. Кривая погрешности при аппроксимации рядом Тейлора
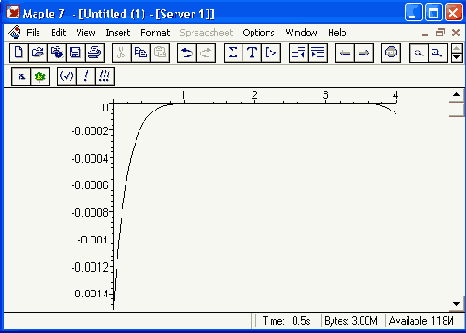
Типичное свойство аппроксимации рядом Тейлора состоит в том, что ошибка мала вблизи точки разложения и велика вдали от нее. В данном случае самая большая ошибка имеет место в левой оконечной точке. Чтобы вычислить значение ошибки в точке х =0, что ведет к делению на нуль (см. определение для f(x)), мы должны использовать значение предела:
> maxTaylorError := abs( Limit(f(x), х-0) - ТауlorАрргох(0) );
 maxTaylorError := .0015029620
Итак, в самом начале наших попыток мы потерпели полное фиаско. Но отчаиваться не стоит, ибо, как говорят, «даже у хорошей хозяйки первый блин — комом».





Шаг 3

Рисунок 17.3. Кривая погрешности при Паде- аппроксимации степени (4,4)
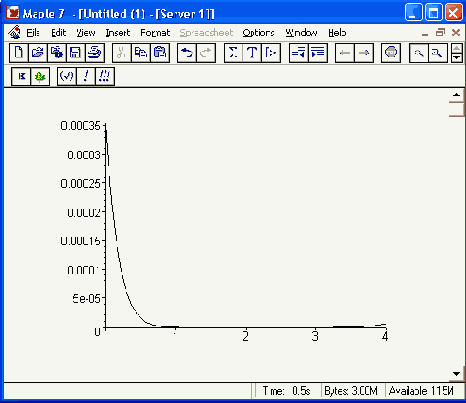
Как и при аппроксимации рядом Тейлора, ошибка здесь мала вблизи точки разложения и велика вдали от нее. Мы снова видим из графика, что для указанной функции, самая большая ошибка — в левой оконечной точке. Однако максимальная ошибка в Паде- аппроксимации уже на порядок меньше, чем при аппроксимации полиномом Тейлора:



Содержание раздела

---

---