Теперь построим графики траекторий для

Шаг 6

Рисунок 17.6. Баллистические траектории камня с массой 500 г
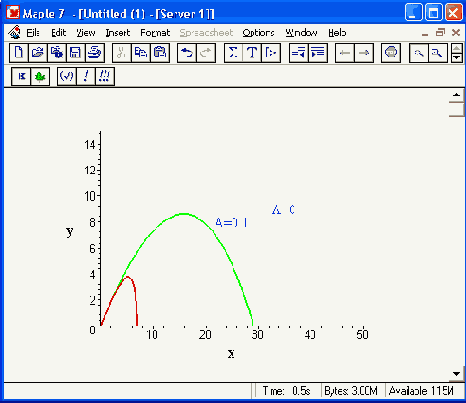
Теперь построим графики траекторий для второго случая:
> display({a3,a4,t1},title='Tpaeкт. полета тела массой 100 г, labels=[x.у], labelfont=[TIMES.ROMAN,14]):
Они представлены на Рисунок 17.7.



Шаг 6

Это тоже довольно громоздкое выражение, и его применение при «ручном» анализе потребовало бы от нас немало изобретательности. Между тем Maple 7 позволяет «в два счета» определить из него амплитудно-частотную (AVM) и фазо- частотную (PhaseAV) характеристики усилителя как функции частоты:
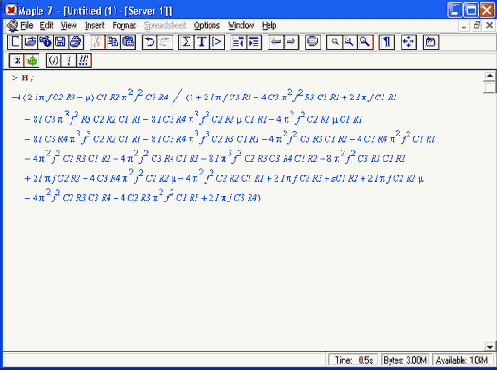
> AVM=-evalc(abs(H)):
> PhaseAV:=evalc(argument(H)):
Преобразуем AVD в логарифмическую характеристику, выражающую усиление в децибелах (dB):
> AVdB:=20*1og10(AVM):
Такая характеристика более привычна для специалистов в радиоэлектронике. Соответственно фазо-частотную характеристику выразим в градусах:
> R2D:=evalf(360/(2*Pi));R2D := 57.29577950
> AVdeg:=R2D*PhaseAV:
Теперь можно перейти к обычным численным расчетам. Зададим конкретные значения компонент эквивалентной схемы усилителя:
> Rl:=100: R2:=100000: R3:=1000: R4:=10000: Cl:=1.*10^(-6): С2:=5*10^(-12): СЗ:=1*10^(-6): mu:=50:
Построим амплитудно-частотную характеристику усилителя:
> gaindata:-NULL:
 phasedata:=NULL:
 for a from 0 to 8 do:
 for i from 2*10^a to l(T(a+l) by 10^a do
 gaindata:=gaindata,  [1. evalf(subs(f=i,AVdB))];
  phasedata:=phasedata, [i, eva1f(subs(f=i,AVdeg))]:
  od: od: 
> 1oglogp1ot([gaindata]. thickness»2, color=black, style=1ine, axes=boxed,
title=`Коэффициент усиления K(f)`,1abels=['Частота (Hz)VK(d8)']):
Она показана на Рисунок 17.13.



Шаг 6

Рисунок 17.22. Временная зависимость выходного сигнала цифрового фильтра
Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:
> Н := array(l..T+l):1i :=array(1..Т+1):
> for n from 0 to T do ,
> ri[n+l] := x[n]*2/T: ii[rn-l] := 0;
> ro[n+l] := y[n]*2/T; Io[rrfl] := 0;
> od:
> FFT(m.ri,ii):rTT(m,ro,io):
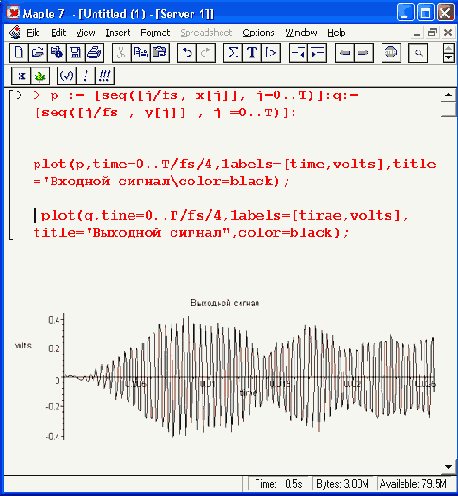
Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:
> р := [seq([j*fs/(T+l),abs(n[j+l]+ii[j-H]*I)],j=0..T/2)]:
> q := [seq([j*fs/(T-H),abs(ro[j-H]+To[j+l]*I)],j=0..T/2)]:
> plot(p, frequency=0..fs/2,y0..0.5,labe1s=[Частотa.V],title='Частотный спектр входного сигнала',color=black);
Этот график представлен на Рисунок 17.23. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.
Теперь построим график спектра выходного сигнала:
> p1ot(q, frequency=0..fs/2,y=0..0.5,labe1s=[Частотa,V], title='Частотный спектр выходного сигнала'бcolor=black);
Он представлен на Рисунок 17.24. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.

Содержание раздела

---

---