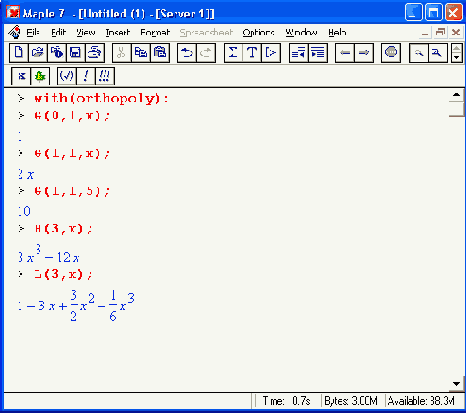
Шаг 1
Шаг 1
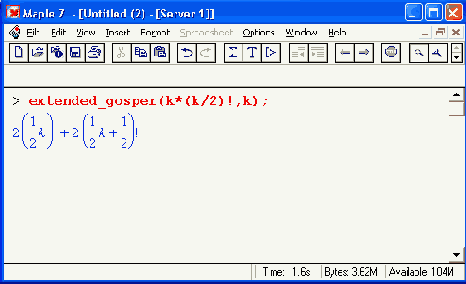
Шаг 1
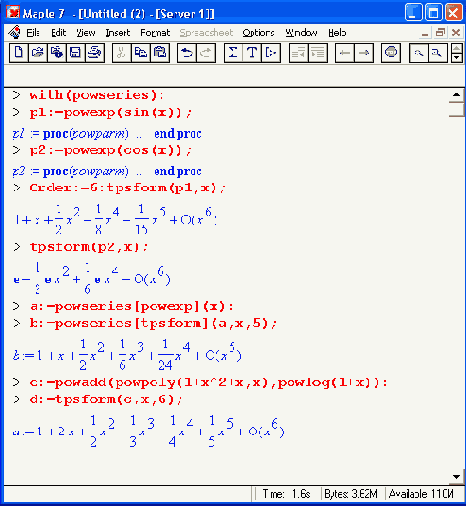
Шаг 1
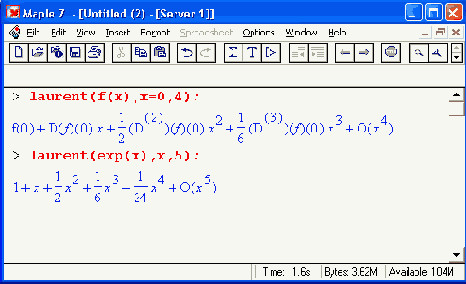
Шаг 1
Шаг 1
Шаг 1
Шаг 1
Шаг 1
laplace(expr,t,p)
Здесь ехрr— преобразуемое выражение, t — переменная, относительно которой записано ехрr, и р — переменная, относительно которой записывается результат преобразования.
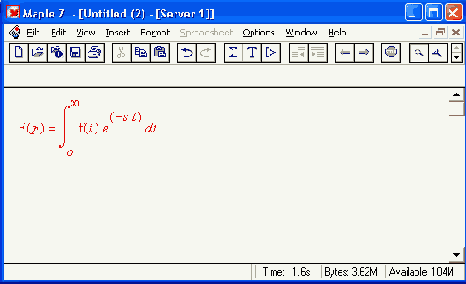
Обратное преобразование Лапласа означает переход от функции F(p) к функции (t) с помощью формулы
Шаг 1
fourier(expr,t,w)
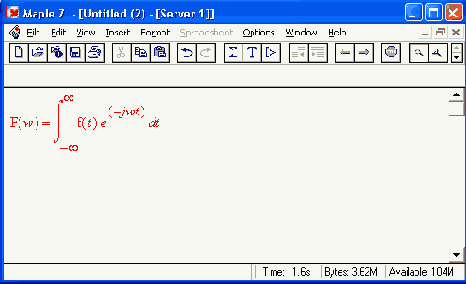
Здесь ехрr — выражение (уравнение или множество), t — переменная, от которой зависит ехрr, и w — переменная, относительно которой записывается результирующая функция. Обратное преобразование Фурье задается вычислением интеграла:
Шаг 1
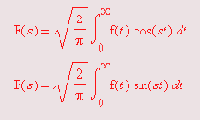
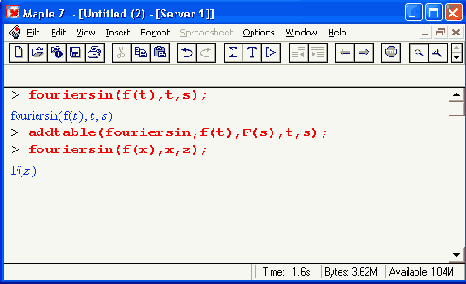
fouriercos(expr,t,s)
fouriersln(expr,t,s)
Поскольку формат задания этих функций вполне очевиден, ограничимся примерами их применения:
Шаг 1
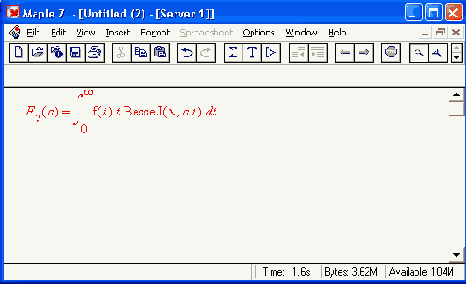
hankel(expr, t, s, nu)
Здесь ехрr — выражение, равенство (или множество, или список с выражениями/равенствами), t — переменная в ехрr, преобразуемая в параметр преобразования s, nu— порядок преобразования. Следующий пример демонстрирует применение функции Ханкеля:
Шаг 1
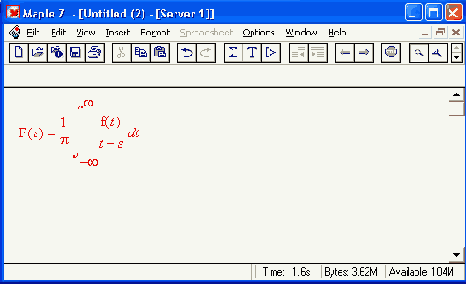
Обратное преобразование Гильберта означает нахождение f(f) по заданной F(s).
Эти преобразования выполняются функциями:
hilbert(expr, t, s)
invhilbert(expr, t,s)
где назначение параметров очевидно.
Приведенные ниже примеры иллюстрируют выполнение этих преобразований:
Шаг 1
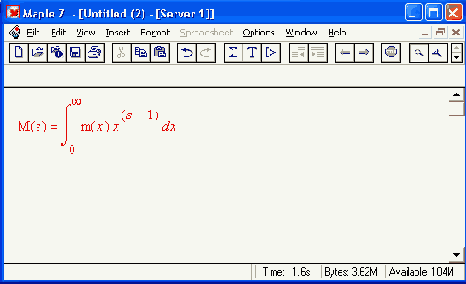
mellin(expr, х, s)
с очевидными параметрами ехрr, х и s.
Применение преобразования Меллина иллюстрируют следующие примеры:
Шаг 1
Шаг 1
Шаг 1
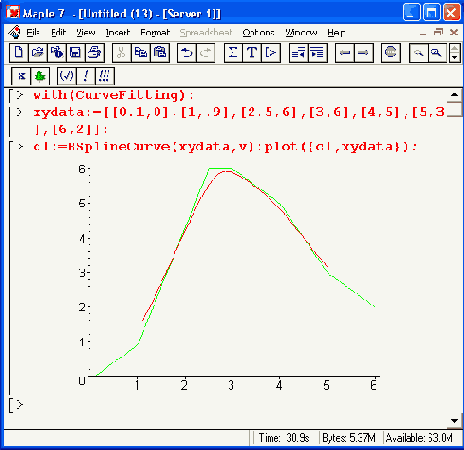
Шаг 1
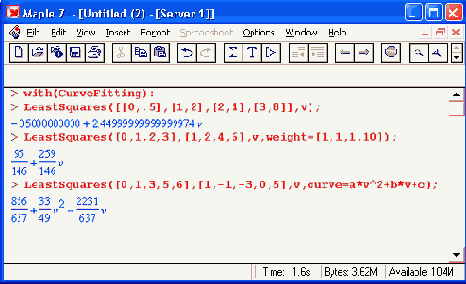
Шаг 1
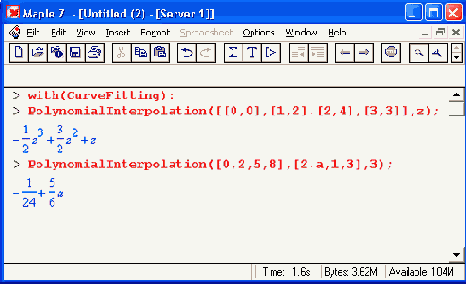
Шаг 1
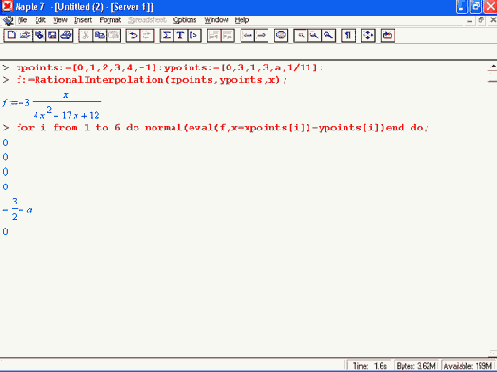
Шаг 1
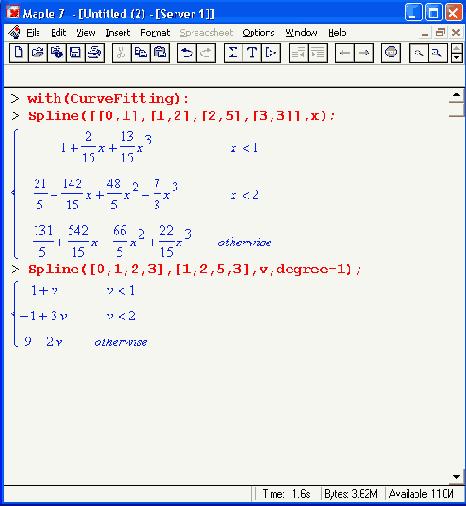
Шаг 1
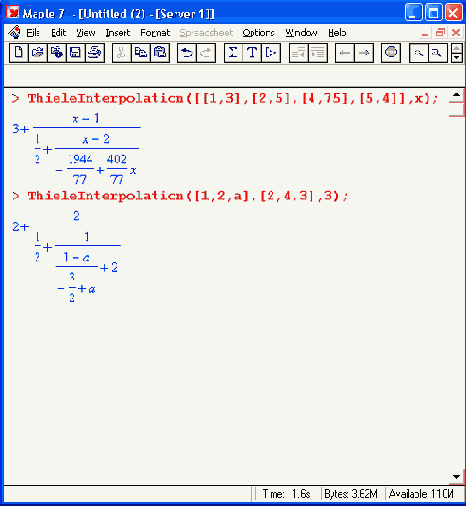
Шаг 1
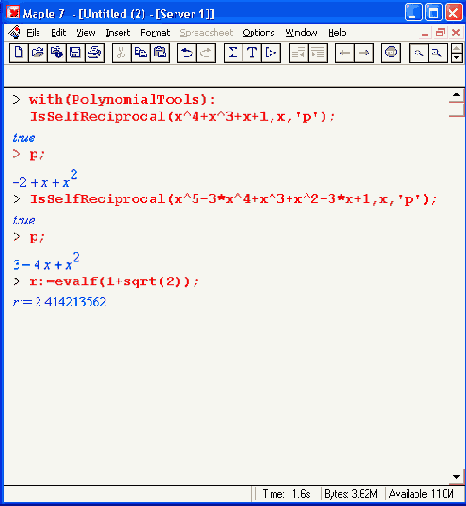
Шаг 1
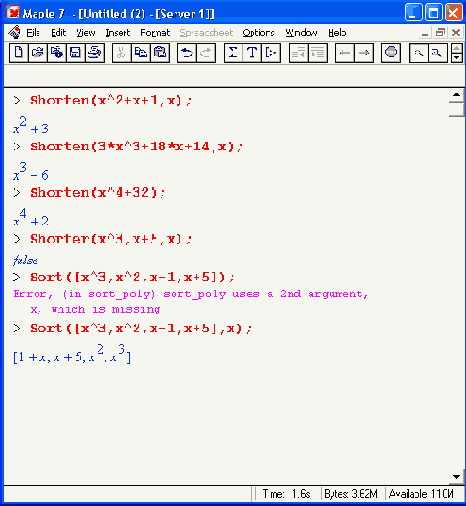
Шаг 1
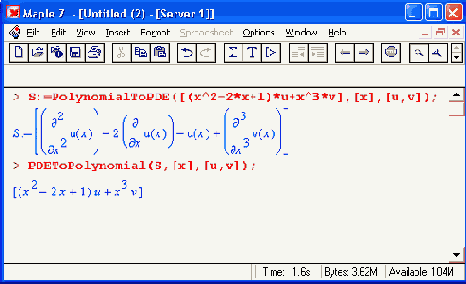
Шаг 1
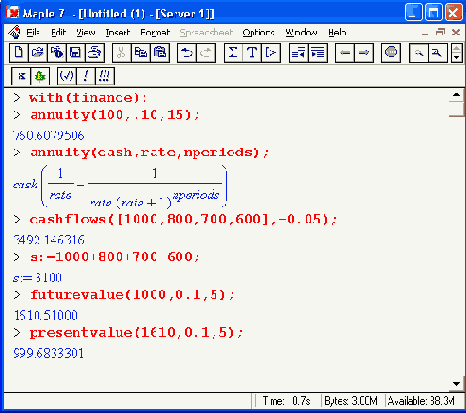
Расчеты такого рода для Maple 7 относятся к достаточно простым, так что даже начинающий пользователь может составить свои функции для таких расчетов по вполне понятным ему и апробированным формулам. Надо отметить, однако, что, используя символьное задание параметров функций, легко получить вывод именно тех формул, которые использует система Maple, и сравнить их со своими формулами. В случае совпадения применение функций Maple возможно и предпочтительно.
Примечание 1
Примечание 1
В целом применение Maple 7 как системы с символьной и точной арифметикой весьма предпочтительно в финансово-экономических и статистических расчетах, поскольку обеспечивает принципиально повышенную точность и устойчивость таких расчетов.
Шаг 1