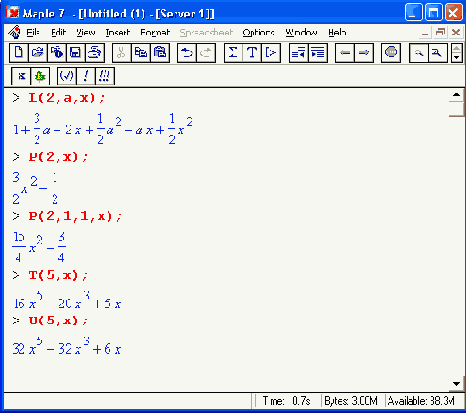
Из этих примеров применение функций

Шаг 2

Из этих примеров применение функций данного пакета достаточно очевидно.



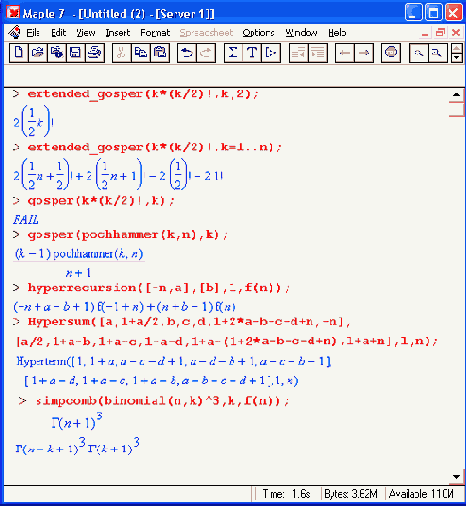
Шаг 2

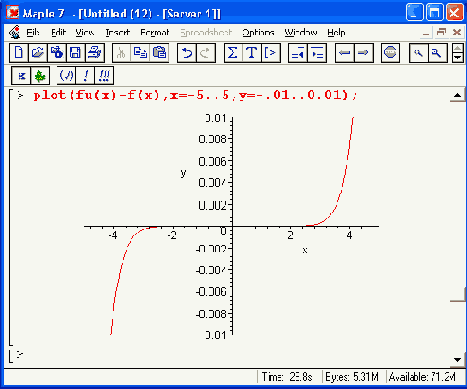
Рисунок 14.4. Аппроксимация Паде для синусоидальной функции



Шаг 2

Для вычисления этого интеграла служит функция:
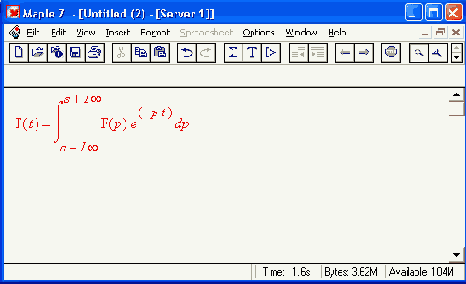
invlaplace(expr,p, t)
где ехрr — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение а обратное —оригинал функции. Ниже приведены примеры применения прямого и обратного преобразований Лапласа:



Шаг 2

Оно фактически переводит представление сигнала из частотной области во временную. Примеры применения преобразования Фурье представлены ниже:



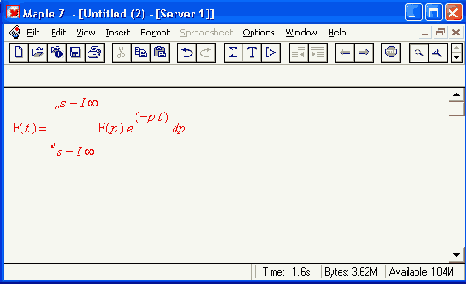
Шаг 2





Шаг 2





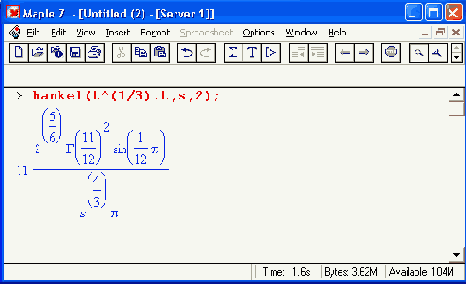
Шаг 2

 

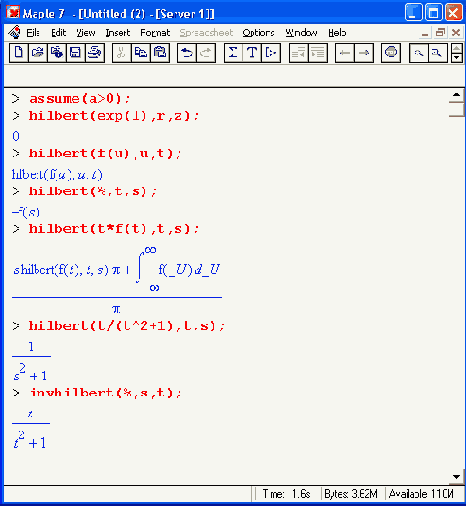
Шаг 2

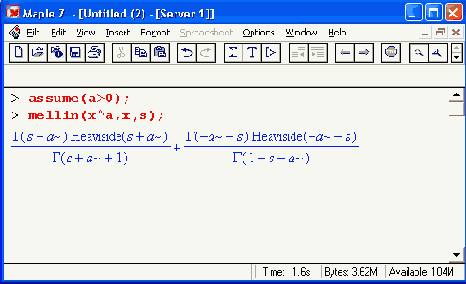
Шаг 2

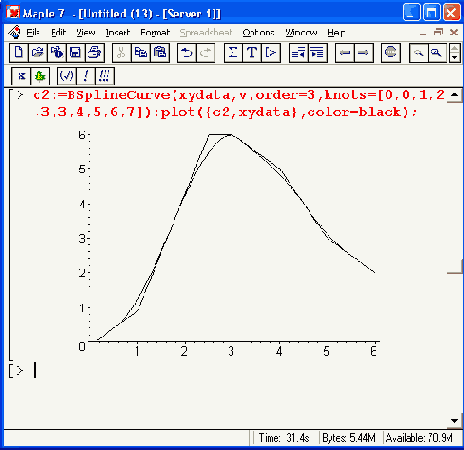
Рисунок 14.6. Применение функции BSplineCurve
Следует отметить, что при малом, числе точек аппроксимация В-сплайнами дает невысокую точность, что и видно из Рисунок 14.6



Шаг 2

Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — необязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {tl,... ,tm}, таких что полином а расщепляется над K=Q(tl,... ,tm), где Q означает поле рациональных чисел. Примеры:



Шаг 2

Представляет интерес построение графиков ортогональных многочленов. На Рисунок 14.1 построены графики ряда многочленов Гегенбауэра и Эрмита.

Содержание раздела

---

---