Двухслойная схема пристенной турбулентности
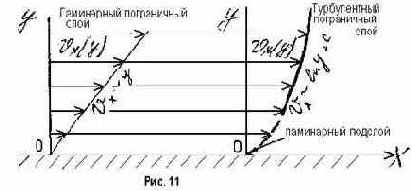
Чтобы подчеркнуть главную особенность турбулентного движения около твердой стенки, рассмотрим установившееся движение жидкости вдоль безграничной пластины ['7]. Расположим ось координат так, чтобы ось х была направлена вдоль пластины, а ось у - по нормали к ней (рис. 11). При такой идеализации течения, когда поток совершает плоское стационарное осредненное движение при отсутствии массовых сил, любые два сечения, перпендикулярные линиям тока, идентичны в кинематическом и динамическом смысле. Это позволяет полагать все производные по X равными нулю, компоненты скорости



Сравним между собой ламинарное и осредненное турбулентное движения такого типа.
Замечая, что ux=ux(y); uy=uz=0; p=p(y), получим уравнения Навье -Стокса ламинарного движения в виде:
а)

б)

Проинтегрируем эти уравнения, преобразовав (2.17) к виду:
а)


б) р=const.
После повторного интегрирования уравнения (2.17) распределение скоростей ux(y) в ламинарном потоке будет:

При y=0 ux=0, т.е. на стенке скорость обращается в нуль, что дает постоянную интегрирования С2=0.
Тогда получаем следующее распределение скоростей ux(y) в ламинарном потоке:

Это свидетельствует о линейном профиле скоростей в ламинарном потоке и о постоянстве напряжения трения между любыми слоями в осредненном движении, равного напряжению трения на стенке:

Перейдем теперь к турбулентному движению, описываемому в нашем случае уравнением Рейнольдса. Будет считать, что для безграничной пластины все параметры потока не зависят от х. Отбросив черточки над осредненными величинами скоростей (поскольку рассматривается осредненное движение), получим уравнение Рейнольдса осредненного движения несжимаемой вязкой жидкости.
В исходном виде уравнение Рейнольдса движения несжимаемой вязкой жидкости имеет вид:

Так как все производные по Х равны нулю (поскольку все параметры потока не зависят от Х); uy=0 для тонкой пластины, то, опуская черточки над uх, получаем:
Тогда формула для турбулентного напряжения трения, называемая формулой Прандтля, имеет вид:

где l - длина перемешивания, характеризующая собой масштаб турбулентности (т.е. средний размер связанных объемов жидкостей, участвующих в турбулентном переносе).
Замечая, что расстояние "у'' данной точки от твердой стенки представляет собой единственную характерную для этой точки в безграничном потоке длину, Прандтль предложил наиболее простую зависимость
l=æ×у,
где æ - коэффициент пропорциональности (числовая константа, определяемая из опыта). Необходимо отметить, что эта формула имеет место лишь в пристеночной области. Подставив эту зависимость в формулу ( 2.24), получим:

Решая это уравнение относительно


Этот так называемый логарифмический профиль скоростей в турбулентном потоке существенно отличается от ламинарного линейного распределения скоростей вблизи стенки.
Так как последняя формула была выведена в предположении, что исследуется движение на некотором расстоянии от стенки, то она может и не удовлетворяться при у=0 и, следовательно, нельзя находить произвольную постоянную "С"- из граничных условий на стенке. Действительно, при у = 0 скорость


Согласно прежним рассуждениям, будем искать такое расстояние от стенки у=dл, для которого при у<dл существенно преобладает вязкое трение, а при у>dл - турбулентное трение, т.е. при у<dл движение будет ламинарным, а при у>dл - турбулентным. Величина dл называется толщиной ламинарного вязкого подслоя. В действительности такой резкой границы между пристеночным подслоем ламинарного движения и областью турбулентного движения не существует.